2021
Marco, A., Baumann, D., Khadiv, M., Hennig, P., Righetti, L., Trimpe, S.
Robot Learning with Crash Constraints
IEEE Robotics and Automation Letters, 6(2):1439-1446, IEEE, February 2021 (article)
2020
Stockinger, G., Janka, H., Kresse, D., Melson, T., Ertl, T., Gabler, M., Gessner, A., Wongwathanarat, A., Tolstov, A., Leung, S., Nomoto, K., Heger, A.
Three-dimensional models of core-collapse supernovae from low-mass progenitors with implications for Crab
Monthly Notices of the Royal Astronomical Society , 496(2):2039-2084, August 2020 (article)
Kanagawa, M., Sriperumbudur, B. K., Fukumizu, K.
Convergence Analysis of Deterministic Kernel-Based Quadrature Rules in Misspecified Settings
Foundations of Computational Mathematics, 20, pages: 155-1944, February 2020 (article)
Kersting, H., Sullivan, T. J., Hennig, P.
Convergence rates of Gaussian ODE filters
Statistics and Computing, 30(6):1791-1816, 2020 (article)
Wahl, N., Hennig, P., Wieser, H., Bangert, M.
Analytical probabilistic modeling of dose-volume histograms
Medical Physics, 47(10):5260-5273, 2020 (article)
2019
Kunstner, F., Hennig, P., Balles, L.
Limitations of the empirical Fisher approximation for natural gradient descent
Advances in Neural Information Processing Systems 32 (NeurIPS 2019), pages: 4158-4169, (Editors: H. Wallach and H. Larochelle and A. Beygelzimer and F. d’Alché-Buc and E. Fox and R. Garnett), Curran Associates, Inc., 33rd Annual Conference on Neural Information Processing Systems, December 2019 (conference)
Kanagawa, M., Hennig, P.
Convergence Guarantees for Adaptive Bayesian Quadrature Methods
Advances in Neural Information Processing Systems 32 (NeurIPS 2019), pages: 6234-6245, (Editors: H. Wallach and H. Larochelle and A. Beygelzimer and F. d’Alché-Buc and E. Fox and R. Garnett), Curran Associates, Inc., 33rd Annual Conference on Neural Information Processing Systems, December 2019 (conference)
Tronarp, F., Kersting, H., Särkkä, S., Hennig, P.
Probabilistic Solutions To Ordinary Differential Equations As Non-Linear Bayesian Filtering: A New Perspective
Statistics and Computing, 29(6):1297-1315, 2019 (article)
Gessner, A. G. J. M. M.
Active Multi-Information Source Bayesian Quadrature
Proceedings 35TH UNCERTAINTY IN ARTIFICIAL INTELLIGENCE CONFERENCE (UAI 2019), pages: 712-721, (Editors: Adams, RP; Gogate, V), UAI 2019, July 2019 (conference)
Schneider, F., Balles, L., Hennig, P.
DeepOBS: A Deep Learning Optimizer Benchmark Suite
7th International Conference on Learning Representations (ICLR), May 2019 (conference)
de Roos, F., Hennig, P.
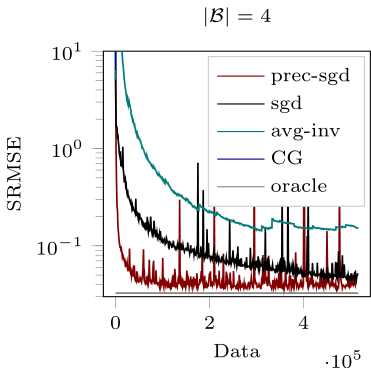
Active Probabilistic Inference on Matrices for Pre-Conditioning in Stochastic Optimization
Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics (AISTATS), 89, pages: 1448-1457, (Editors: Kamalika Chaudhuri and Masashi Sugiyama), PMLR, April 2019 (conference)
Arvanitidis, G., Hauberg, S., Hennig, P., Schober, M.
Fast and Robust Shortest Paths on Manifolds Learned from Data
Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics (AISTATS), 89, pages: 1506-1515, (Editors: Kamalika Chaudhuri and Masashi Sugiyama), PMLR, April 2019 (conference)
Karvonen, T., Kanagawa, M., Särkä, S.
On the positivity and magnitudes of Bayesian quadrature weights
Statistics and Computing, 29, pages: 1317-1333, 2019 (article)
Tronarp, F., Kersting, H., Särkkä, S. H. P.
Probabilistic solutions to ordinary differential equations as nonlinear Bayesian filtering: a new perspective
Statistics and Computing, 29(6):1297-1315, 2019 (article)
Motta, A., Berning, M., Boergens, K. M., Staffler, B., Beining, M., Loomba, S., Hennig, P., Wissler, H., Helmstaedter, M.
Dense connectomic reconstruction in layer 4 of the somatosensory cortex
Science, 366(6469):eaay3134, 2019 (article)
Bartels, S., Cockayne, J., Ipsen, I., Hennig, P.
Probabilistic Linear Solvers: A Unifying View
Statistics and Computing, 29(6):1249-1263, 2019 (article)
2018
Kajihara, T., Kanagawa, M., Yamazaki, K., Fukumizu, K.
Kernel Recursive ABC: Point Estimation with Intractable Likelihood
Proceedings of the 35th International Conference on Machine Learning, pages: 2405-2414, PMLR, July 2018 (conference)
Balles, L., Hennig, P.
Dissecting Adam: The Sign, Magnitude and Variance of Stochastic Gradients
Proceedings of the 35th International Conference on Machine Learning (ICML), 80, pages: 404-413, Proceedings of Machine Learning Research, (Editors: Jennifer Dy and Andreas Krause), PMLR, ICML, July 2018 (conference)
Kersting, H., Sullivan, T. J., Hennig, P.
Convergence Rates of Gaussian ODE Filters
arXiv preprint 2018, arXiv:1807.09737 [math.NA], July 2018 (article)
Muandet, K., Kanagawa, M., Saengkyongam, S., Marukata, S.
Counterfactual Mean Embedding: A Kernel Method for Nonparametric Causal Inference
Workshop on Machine Learning for Causal Inference, Counterfactual Prediction, and Autonomous Action (CausalML) at ICML, July 2018 (conference)
Kanagawa, M., Hennig, P., Sejdinovic, D., Sriperumbudur, B. K.
Gaussian Processes and Kernel Methods: A Review on Connections and Equivalences
Arxiv e-prints, arXiv:1805.08845v1 [stat.ML], 2018 (article)
Muandet, K., Kanagawa, M., Saengkyongam, S., Marukata, S.
Counterfactual Mean Embedding: A Kernel Method for Nonparametric Causal Inference
Arxiv e-prints, arXiv:1805.08845v1 [stat.ML], 2018 (article)
Nishiyama, Y., Kanagawa, M., Gretton, A., Fukumizu, K.
Model-based Kernel Sum Rule: Kernel Bayesian Inference with Probabilistic Models
Arxiv e-prints, arXiv:1409.5178v2 [stat.ML], 2018 (article)
Schober, M., Särkkä, S., Hennig, P.
A probabilistic model for the numerical solution of initial value problems
Statistics and Computing, 29(1):99–122, 2018 (article)
Mahsereci, M.
Probabilistic Approaches to Stochastic Optimization
Eberhard Karls Universität Tübingen, Germany, 2018 (phdthesis)
Wahl, N., Hennig, P., Wieser, H., Bangert, M.
Analytical incorporation of fractionation effects in probabilistic treatment planning for intensity-modulated proton therapy
Medical Physics, 45(4):1317-1328, 2018 (article)
Garreau, D., Jitkrittum, W., Kanagawa, M.
Large sample analysis of the median heuristic
2018 (misc) In preparation
Schober, M.
Probabilistic Ordinary Differential Equation Solvers — Theory and Applications
Eberhard Karls Universität Tübingen, Germany, 2018 (phdthesis)
2017
Marco, A., Hennig, P., Schaal, S., Trimpe, S.
On the Design of LQR Kernels for Efficient Controller Learning
Proceedings of the 56th IEEE Annual Conference on Decision and Control (CDC), pages: 5193-5200, IEEE, IEEE Conference on Decision and Control, December 2017 (conference)
Mahsereci, M., Hennig, P.
Probabilistic Line Searches for Stochastic Optimization
Journal of Machine Learning Research, 18(119):1-59, November 2017 (article)
Balles, L., Romero, J., Hennig, P.
Coupling Adaptive Batch Sizes with Learning Rates
In Proceedings of the 33rd Conference on Uncertainty in Artificial Intelligence (UAI), pages: ID 141, (Editors: Gal Elidan, Kristian Kersting, and Alexander T. Ihler), August 2017 (inproceedings)
Schober, M., Adam, A., Yair, O., Mazor, S., Nowozin, S.
Dynamic Time-of-Flight
Proceedings IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2017, pages: 170-179, IEEE, Piscataway, NJ, USA, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), July 2017 (conference)
Marco, A., Berkenkamp, F., Hennig, P., Schoellig, A. P., Krause, A., Schaal, S., Trimpe, S.
Virtual vs. Real: Trading Off Simulations and Physical Experiments in Reinforcement Learning with Bayesian Optimization
In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), pages: 1557-1563, IEEE, Piscataway, NJ, USA, May 2017 (inproceedings)
Klein, A., Falkner, S., Bartels, S., Hennig, P., Hutter, F.
Fast Bayesian Optimization of Machine Learning Hyperparameters on Large Datasets
Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS), 54, pages: 528-536, Proceedings of Machine Learning Research, (Editors: Sign, Aarti and Zhu, Jerry), PMLR, April 2017 (conference)
Mahsereci, M., Balles, L., Lassner, C., Hennig, P.
Early Stopping Without a Validation Set
arXiv preprint arXiv:1703.09580, 2017 (article)
Roos, F. D., Hennig, P.
Krylov Subspace Recycling for Fast Iterative Least-Squares in Machine Learning
arXiv preprint arXiv:1706.00241, 2017 (article)
Klein, A., Falkner, S., Bartels, S., Hennig, P., Hutter, F.
Fast Bayesian hyperparameter optimization on large datasets
Electronic Journal of Statistics, 11, 2017 (article)
Klenske, E. D.
Nonparametric Disturbance Correction and Nonlinear Dual Control
(24098), ETH Zurich, 2017 (phdthesis)
Gretton, A., Hennig, P., Rasmussen, C., Schölkopf, B.
New Directions for Learning with Kernels and Gaussian Processes (Dagstuhl Seminar 16481)
Dagstuhl Reports, 6(11):142-167, 2017 (article)
Wahl, N., Hennig, P., Wieser, H. P., Bangert, M.
Efficiency of analytical and sampling-based uncertainty propagation in intensity-modulated proton therapy
Physics in Medicine & Biology, 62(14):5790-5807, 2017 (article)
Wieser, H., Hennig, P., Wahl, N., Bangert, M.
Analytical probabilistic modeling of RBE-weighted dose for ion therapy
Physics in Medicine and Biology (PMB), 62(23):8959-8982, 2017 (article)
2016
Klenske, E. D., Hennig, P., Schölkopf, B., Zeilinger, M. N.
Approximate dual control maintaining the value of information with an application to building control
In European Control Conference (ECC), pages: 800-806, June 2016 (inproceedings)
Kersting, H., Hennig, P.
Active Uncertainty Calibration in Bayesian ODE Solvers
Proceedings of the 32nd Conference on Uncertainty in Artificial Intelligence (UAI), pages: 309-318, (Editors: Ihler, Alexander T. and Janzing, Dominik), June 2016 (conference)
Marco, A., Hennig, P., Bohg, J., Schaal, S., Trimpe, S.
Automatic LQR Tuning Based on Gaussian Process Global Optimization
In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), pages: 270-277, IEEE, IEEE International Conference on Robotics and Automation, May 2016 (inproceedings)
González, J., Dai, Z., Hennig, P., Lawrence, N.
Batch Bayesian Optimization via Local Penalization
Proceedings of the 19th International Conference on Artificial Intelligence and Statistics (AISTATS), 51, pages: 648-657, JMLR Workshop and Conference Proceedings, (Editors: Gretton, A. and Robert, C. C.), May 2016 (conference)
Bartels, S., Hennig, P.
Probabilistic Approximate Least-Squares
Proceedings of the 19th International Conference on Artificial Intelligence and Statistics (AISTATS), 51, pages: 676-684, JMLR Workshop and Conference Proceedings, (Editors: Gretton, A. and Robert, C. C. ), May 2016 (conference)
Klenske, E. D., Zeilinger, M., Schölkopf, B., Hennig, P.
Gaussian Process-Based Predictive Control for Periodic Error Correction
IEEE Transactions on Control Systems Technology , 24(1):110-121, 2016 (article)
Klenske, E. D., Hennig, P.
Dual Control for Approximate Bayesian Reinforcement Learning
Journal of Machine Learning Research, 17(127):1-30, 2016 (article)
2015
Marco, A., Hennig, P., Bohg, J., Schaal, S., Trimpe, S.
Automatic LQR Tuning Based on Gaussian Process Optimization: Early Experimental Results
Machine Learning in Planning and Control of Robot Motion Workshop at the IEEE/RSJ International Conference on Intelligent Robots and Systems (iROS), pages: , , Machine Learning in Planning and Control of Robot Motion Workshop, October 2015 (conference)