2019
Kunstner, F., Hennig, P., Balles, L.
Limitations of the empirical Fisher approximation for natural gradient descent
Advances in Neural Information Processing Systems 32 (NeurIPS 2019), pages: 4158-4169, (Editors: H. Wallach and H. Larochelle and A. Beygelzimer and F. d’Alché-Buc and E. Fox and R. Garnett), Curran Associates, Inc., 33rd Annual Conference on Neural Information Processing Systems, December 2019 (conference)
Kanagawa, M., Hennig, P.
Convergence Guarantees for Adaptive Bayesian Quadrature Methods
Advances in Neural Information Processing Systems 32 (NeurIPS 2019), pages: 6234-6245, (Editors: H. Wallach and H. Larochelle and A. Beygelzimer and F. d’Alché-Buc and E. Fox and R. Garnett), Curran Associates, Inc., 33rd Annual Conference on Neural Information Processing Systems, December 2019 (conference)
Gessner, A. G. J. M. M.
Active Multi-Information Source Bayesian Quadrature
Proceedings 35TH UNCERTAINTY IN ARTIFICIAL INTELLIGENCE CONFERENCE (UAI 2019), pages: 712-721, (Editors: Adams, RP; Gogate, V), UAI 2019, July 2019 (conference)
Schneider, F., Balles, L., Hennig, P.
DeepOBS: A Deep Learning Optimizer Benchmark Suite
7th International Conference on Learning Representations (ICLR), May 2019 (conference)
de Roos, F., Hennig, P.
Active Probabilistic Inference on Matrices for Pre-Conditioning in Stochastic Optimization
Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics (AISTATS), 89, pages: 1448-1457, (Editors: Kamalika Chaudhuri and Masashi Sugiyama), PMLR, April 2019 (conference)
Arvanitidis, G., Hauberg, S., Hennig, P., Schober, M.
Fast and Robust Shortest Paths on Manifolds Learned from Data
Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics (AISTATS), 89, pages: 1506-1515, (Editors: Kamalika Chaudhuri and Masashi Sugiyama), PMLR, April 2019 (conference)
2018
Kajihara, T., Kanagawa, M., Yamazaki, K., Fukumizu, K.
Kernel Recursive ABC: Point Estimation with Intractable Likelihood
Proceedings of the 35th International Conference on Machine Learning, pages: 2405-2414, PMLR, July 2018 (conference)
Balles, L., Hennig, P.
Dissecting Adam: The Sign, Magnitude and Variance of Stochastic Gradients
Proceedings of the 35th International Conference on Machine Learning (ICML), 80, pages: 404-413, Proceedings of Machine Learning Research, (Editors: Jennifer Dy and Andreas Krause), PMLR, ICML, July 2018 (conference)
Muandet, K., Kanagawa, M., Saengkyongam, S., Marukata, S.
Counterfactual Mean Embedding: A Kernel Method for Nonparametric Causal Inference
Workshop on Machine Learning for Causal Inference, Counterfactual Prediction, and Autonomous Action (CausalML) at ICML, July 2018 (conference)
2017
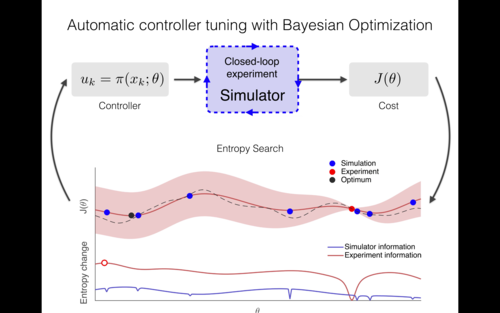
Marco, A., Hennig, P., Schaal, S., Trimpe, S.
On the Design of LQR Kernels for Efficient Controller Learning
Proceedings of the 56th IEEE Annual Conference on Decision and Control (CDC), pages: 5193-5200, IEEE, IEEE Conference on Decision and Control, December 2017 (conference)
Balles, L., Romero, J., Hennig, P.
Coupling Adaptive Batch Sizes with Learning Rates
In Proceedings of the 33rd Conference on Uncertainty in Artificial Intelligence (UAI), pages: ID 141, (Editors: Gal Elidan, Kristian Kersting, and Alexander T. Ihler), August 2017 (inproceedings)
Schober, M., Adam, A., Yair, O., Mazor, S., Nowozin, S.
Dynamic Time-of-Flight
Proceedings IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2017, pages: 170-179, IEEE, Piscataway, NJ, USA, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), July 2017 (conference)
Marco, A., Berkenkamp, F., Hennig, P., Schoellig, A. P., Krause, A., Schaal, S., Trimpe, S.
Virtual vs. Real: Trading Off Simulations and Physical Experiments in Reinforcement Learning with Bayesian Optimization
In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), pages: 1557-1563, IEEE, Piscataway, NJ, USA, May 2017 (inproceedings)
Klein, A., Falkner, S., Bartels, S., Hennig, P., Hutter, F.
Fast Bayesian Optimization of Machine Learning Hyperparameters on Large Datasets
Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS), 54, pages: 528-536, Proceedings of Machine Learning Research, (Editors: Sign, Aarti and Zhu, Jerry), PMLR, April 2017 (conference)
2016
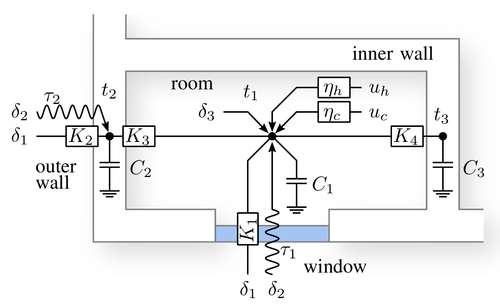
Klenske, E. D., Hennig, P., Schölkopf, B., Zeilinger, M. N.
Approximate dual control maintaining the value of information with an application to building control
In European Control Conference (ECC), pages: 800-806, June 2016 (inproceedings)
Kersting, H., Hennig, P.
Active Uncertainty Calibration in Bayesian ODE Solvers
Proceedings of the 32nd Conference on Uncertainty in Artificial Intelligence (UAI), pages: 309-318, (Editors: Ihler, Alexander T. and Janzing, Dominik), June 2016 (conference)
Marco, A., Hennig, P., Bohg, J., Schaal, S., Trimpe, S.
Automatic LQR Tuning Based on Gaussian Process Global Optimization
In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), pages: 270-277, IEEE, IEEE International Conference on Robotics and Automation, May 2016 (inproceedings)
González, J., Dai, Z., Hennig, P., Lawrence, N.
Batch Bayesian Optimization via Local Penalization
Proceedings of the 19th International Conference on Artificial Intelligence and Statistics (AISTATS), 51, pages: 648-657, JMLR Workshop and Conference Proceedings, (Editors: Gretton, A. and Robert, C. C.), May 2016 (conference)
Bartels, S., Hennig, P.
Probabilistic Approximate Least-Squares
Proceedings of the 19th International Conference on Artificial Intelligence and Statistics (AISTATS), 51, pages: 676-684, JMLR Workshop and Conference Proceedings, (Editors: Gretton, A. and Robert, C. C. ), May 2016 (conference)
2015
Marco, A., Hennig, P., Bohg, J., Schaal, S., Trimpe, S.
Automatic LQR Tuning Based on Gaussian Process Optimization: Early Experimental Results
Machine Learning in Planning and Control of Robot Motion Workshop at the IEEE/RSJ International Conference on Intelligent Robots and Systems (iROS), pages: , , Machine Learning in Planning and Control of Robot Motion Workshop, October 2015 (conference)
Sgouritsa, E., Janzing, D., Hennig, P., Schölkopf, B.
Inference of Cause and Effect with Unsupervised Inverse Regression
In Proceedings of the 18th International Conference on Artificial Intelligence and Statistics, 38, pages: 847-855, JMLR Workshop and Conference Proceedings, (Editors: Lebanon, G. and Vishwanathan, S.V.N.), JMLR.org, AISTATS, 2015 (inproceedings)
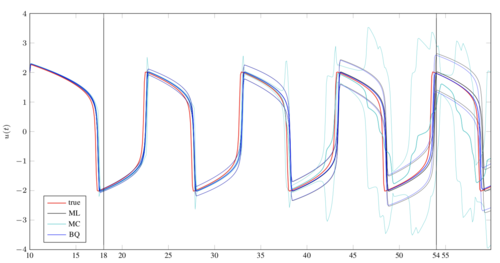
Mahsereci, M., Hennig, P.
Probabilistic Line Searches for Stochastic Optimization
In Advances in Neural Information Processing Systems 28, pages: 181-189, (Editors: C. Cortes, N.D. Lawrence, D.D. Lee, M. Sugiyama and R. Garnett), Curran Associates, Inc., 29th Annual Conference on Neural Information Processing Systems (NIPS), 2015 (inproceedings)
Hauberg, S., Schober, M., Liptrot, M., Hennig, P., Feragen, A.
A Random Riemannian Metric for Probabilistic Shortest-Path Tractography
In 18th International Conference on Medical Image Computing and Computer Assisted Intervention, 9349, pages: 597-604, Lecture Notes in Computer Science, MICCAI, 2015 (inproceedings)
2014
Kiefel, M., Schuler, C., Hennig, P.
Probabilistic Progress Bars
In Conference on Pattern Recognition (GCPR), 8753, pages: 331-341, Lecture Notes in Computer Science, (Editors: Jiang, X., Hornegger, J., and Koch, R.), Springer, GCPR, September 2014 (inproceedings)
Hennig, P., Hauberg, S.
Probabilistic Solutions to Differential Equations and their Application to Riemannian Statistics
In Proceedings of the 17th International Conference on Artificial Intelligence and Statistics, 33, pages: 347-355, JMLR: Workshop and Conference Proceedings, (Editors: S Kaski and J Corander), Microtome Publishing, Brookline, MA, AISTATS, April 2014 (inproceedings)
Schober, M., Duvenaud, D., Hennig, P.
Probabilistic ODE Solvers with Runge-Kutta Means
In Advances in Neural Information Processing Systems 27, pages: 739-747, (Editors: Z. Ghahramani, M. Welling, C. Cortes, N.D. Lawrence and K.Q. Weinberger), Curran Associates, Inc., 28th Annual Conference on Neural Information Processing Systems (NIPS), 2014 (inproceedings)
Garnett, R., Osborne, M., Hennig, P.
Active Learning of Linear Embeddings for Gaussian Processes
In Proceedings of the 30th Conference on Uncertainty in Artificial Intelligence, pages: 230-239, (Editors: NL Zhang and J Tian), AUAI Press , Corvallis, Oregon, UAI2014, 2014, another link: http://arxiv.org/abs/1310.6740 (inproceedings)
Schober, M., Kasenburg, N., Feragen, A., Hennig, P., Hauberg, S.
Probabilistic Shortest Path Tractography in DTI Using Gaussian Process ODE Solvers
In Medical Image Computing and Computer-Assisted Intervention – MICCAI 2014, Lecture Notes in Computer Science Vol. 8675, pages: 265-272, (Editors: P. Golland, N. Hata, C. Barillot, J. Hornegger and R. Howe), Springer, Heidelberg, MICCAI, 2014 (inproceedings)
Gunter, T., Osborne, M., Garnett, R., Hennig, P., Roberts, S.
Sampling for Inference in Probabilistic Models with Fast Bayesian Quadrature
In Advances in Neural Information Processing Systems 27, pages: 2789-2797, (Editors: Z. Ghahramani, M. Welling, C. Cortes, N.D. Lawrence and K.Q. Weinberger), Curran Associates, Inc., 28th Annual Conference on Neural Information Processing Systems (NIPS), 2014 (inproceedings)
Meier, F., Hennig, P., Schaal, S.
Incremental Local Gaussian Regression
In Advances in Neural Information Processing Systems 27, pages: 972-980, (Editors: Z. Ghahramani, M. Welling, C. Cortes, N.D. Lawrence and K.Q. Weinberger), 28th Annual Conference on Neural Information Processing Systems (NIPS), 2014, clmc (inproceedings)
Meier, F., Hennig, P., Schaal, S.
Efficient Bayesian Local Model Learning for Control
In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, pages: 2244 - 2249, IROS, 2014, clmc (inproceedings)
2013
Lopez-Paz, D., Hennig, P., Schölkopf, B.
The Randomized Dependence Coefficient
In Advances in Neural Information Processing Systems 26, pages: 1-9, (Editors: C.J.C. Burges, L. Bottou, M. Welling, Z. Ghahramani, and K.Q. Weinberger), 27th Annual Conference on Neural Information Processing Systems (NIPS), 2013 (inproceedings)
Hennig, P.
Fast Probabilistic Optimization from Noisy Gradients
In Proceedings of The 30th International Conference on Machine Learning, JMLR W&CP 28(1), pages: 62–70, (Editors: S Dasgupta and D McAllester), ICML, 2013 (inproceedings)
Klenske, E., Zeilinger, M., Schölkopf, B., Hennig, P.
Nonparametric dynamics estimation for time periodic systems
In Proceedings of the 51st Annual Allerton Conference on Communication, Control, and Computing, pages: 486-493 , 2013 (inproceedings)
Bangert, M., Hennig, P., Oelfke, U.
Analytical probabilistic proton dose calculation and range uncertainties
In 17th International Conference on the Use of Computers in Radiation Therapy, pages: 6-11, (Editors: A. Haworth and T. Kron), ICCR, 2013 (inproceedings)
2012
Hennig, P., Kiefel, M.
Quasi-Newton Methods: A New Direction
In Proceedings of the 29th International Conference on Machine Learning, pages: 25-32, ICML ’12, (Editors: John Langford and Joelle Pineau), Omnipress, New York, NY, USA, ICML, July 2012 (inproceedings)
Bócsi, B., Hennig, P., Csató, L., Peters, J.
Learning Tracking Control with Forward Models
In pages: 259 -264, IEEE International Conference on Robotics and Automation (ICRA), May 2012 (inproceedings)
Cunningham, J., Hennig, P., Lacoste-Julien, S.
Approximate Gaussian Integration using Expectation Propagation
In pages: 1-11, -, January 2012 (inproceedings) Submitted
Hennig, P., Stern, D., Herbrich, R., Graepel, T.
Kernel Topic Models
In Fifteenth International Conference on Artificial Intelligence and Statistics, 22, pages: 511-519, JMLR Proceedings, (Editors: Lawrence, N. D. and Girolami, M.), JMLR.org, AISTATS , 2012 (inproceedings)
2011
Hennig, P.
Optimal Reinforcement Learning for Gaussian Systems
In Advances in Neural Information Processing Systems 24, pages: 325-333, (Editors: J Shawe-Taylor and RS Zemel and P Bartlett and F Pereira and KQ Weinberger), Twenty-Fifth Annual Conference on Neural Information Processing Systems (NIPS), 2011 (inproceedings)
2010
Bangert, M., Hennig, P., Oelfke, U.
Using an Infinite Von Mises-Fisher Mixture Model to Cluster Treatment Beam Directions in External Radiation Therapy
In pages: 746-751 , (Editors: Draghici, S. , T.M. Khoshgoftaar, V. Palade, W. Pedrycz, M.A. Wani, X. Zhu), IEEE, Piscataway, NJ, USA, Ninth International Conference on Machine Learning and Applications (ICMLA), December 2010 (inproceedings)
Hennig, P., Stern, D., Graepel, T.
Coherent Inference on Optimal Play in Game Trees
In JMLR Workshop and Conference Proceedings Volume 9: AISTATS 2010, pages: 326-333, (Editors: Teh, Y.W. , M. Titterington ), JMLR, Cambridge, MA, USA, Thirteenth International Conference on Artificial Intelligence and Statistics, May 2010 (inproceedings)