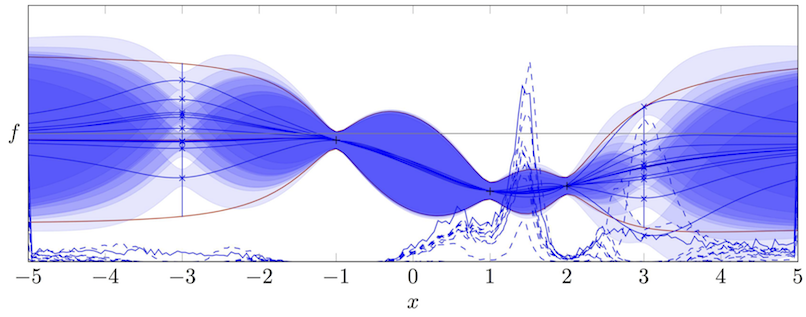
Bayesian Optimization is an increasingly popular approach to industrial and scientific prototyping problems. The basic premise in this setting is that one is looking for a location $x$ in some domain where a fitness function $f(x)$ is (globally) minimized. The additional, sometimes implicit, assumption is that individual evaluations of $f$ have comparably high computational or monetary cost (e.g. because they involve building a physical prototype, or running a robot for a few minutes). To avoid this high cost as much as possible, one thus builds a cheaper surrogate model for the true objective. If this model is probabilistic (i.e. it spreads probability mass over a space of possible true values of the objective) it can be used to reason about which physical experiments would be most useful to perform in pursuit of the true extremum.
Our contribution to this area is the development of a class of Bayesian optimization algorithms, known as Entropy Search [ ] that retain an explicit model for the location of a function's minimum, and reason about changes to this distribution effected by future experiments. Entropy Search is not a cheap method, but it provides a powerful representation in which one can reason about the information content of various kinds of experiments, and take decisions that take into account varying costs and quality of potential experiments.
In recent years, in collaboration with the Intelligent Control Systems group, the Entropy Search framework has been used to build advanced functionality for experimental design in automated machine learning and robotics. This includes the ability to simultaneously and efficiently use and trade off experimental channels of varying fidelity and cost [ ], and the effective use of strong analytical knowledge about a problem [ ].
