NIPS Oral for Michael Schober
PhD student will present his work on probabilistic solvers for differential equations
- 01 December 2014
- Montréal, Canada
- Probabilistic Numerics
Michael Schober' paper on probabilistic solvers for ordinary differential equations has been selected for a full oral presentation at the flagship conference of machine learning.
Michael Schober will present his work on probabilistic solvers for differential equations in front of the 2500-strong plenum at Neural Information Processing Systems in Montréal this week. NIPS is the flagship conference of machine learning, and full orals such as this are only awarded to a handful of papers, about 1% of the submitted works, each year.
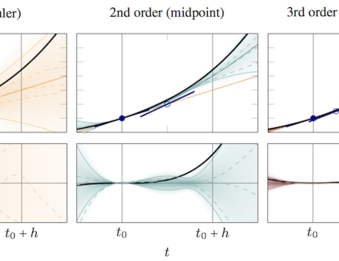
Michael will talk about his work, with David Duvenaud (Cambridge) and Philipp Hennig, constructing a probabilistic algorithm for the solution of ordinary differential equations (full paper on the proceedings page). Classic ODE solvers return point estimates for a curve $x(t)$ solving an equation of the form $$ x(t) = f(x(t),t) $$ Michael and his colleagues showed that Runge-Kutta methods - the oldest and most widely studied class of such algorithms - can also be identified as the maximum a posteriori estimate arising from a particular class of probabilistic regression algorithms. That probabilistic model class has interesting algebraic properties (it consists of Markov processes) that allow for a lightweight implementation. This raises hopes of a robust, fully probabilistic class of solvers that return meaningfully uncertain estimates over the solution of this problem class at a computational complexity comparable to that of classic solvers. ODEs are among the most basic types of numerical problems and feature prominently in many application areas, including control engineering and robotics.